Ha egy statisztikai tankönyvben megnézzük a normális eloszlás definícióját, valami ilyesmit fogunk látni:
Egy folytonos valószínűségi változót normális eloszlásúnak nevezünk m és s paraméterekkel és N(m ,s )-val jelöljük, ha a sűrűségfüggvénye az ábrának megfelelő.
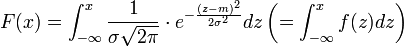
Mond ez valamit egy hétköznapi halandó számára? Nem nagyon.
Nézzük tehát a normális eloszlást közérthetőbb módon.
Ha a nevéből indulunk ki, valami olyan dolog kell hogy legyen, ami a tapasztalatainkkal összhangban van, ismert, nem furcsa - szóval olyan normális. Ha egy emberre ezt mondjuk: normális, akkor nagyjából azt értjük rajta, hogy nincs semmi extrém, szélsőséges benne.
Valami ilyesmire utal ez a kifejezés is: a megszokottra, a "természetesre".
És ez utóbbi szó elég fontos a kifejezés megértésében: a normális eloszlás lényegében a természetes eloszlást jelenti. Nézzünk egy nagyon egyszerű példát:
ha az emberek magasságát nézzük, azt látjuk, hogy az átlagos testmagasság, pontosabban az ahhoz közeli magasság a leggyakoribb. Az utcán viszonylag hasonló magasságú embereket látunk többnyire. Természetesen nem mindenkinek átlagos a magassága: vannak észrevehetően alacsonyabb és magasabb emberek is - ámde ők jóval kevesebben vannak, mint az átlag körüliek.
És vannak természetesen extrém alacsonyak és magasak is - de hát pont azért tartjuk "extrémnek" ezeket a nagyon eltérő magasságokat, mert elég ritkák.
A normális eloszlásnak épp ez a lényege: az átlaghoz közeli, átlag körüli értékek a leggyakoribbak, és ahogy távolodunk az átlagtól, egyre kevesebb eset van - mondhatjuk úgy is, minél jobban eltér valami az átlagtól, annál ritkább.
(Folyt. köv.)
Ha a nevéből indulunk ki, valami olyan dolog kell hogy legyen, ami a tapasztalatainkkal összhangban van, ismert, nem furcsa - szóval olyan normális. Ha egy emberre ezt mondjuk: normális, akkor nagyjából azt értjük rajta, hogy nincs semmi extrém, szélsőséges benne.
Valami ilyesmire utal ez a kifejezés is: a megszokottra, a "természetesre".
És ez utóbbi szó elég fontos a kifejezés megértésében: a normális eloszlás lényegében a természetes eloszlást jelenti. Nézzünk egy nagyon egyszerű példát:
ha az emberek magasságát nézzük, azt látjuk, hogy az átlagos testmagasság, pontosabban az ahhoz közeli magasság a leggyakoribb. Az utcán viszonylag hasonló magasságú embereket látunk többnyire. Természetesen nem mindenkinek átlagos a magassága: vannak észrevehetően alacsonyabb és magasabb emberek is - ámde ők jóval kevesebben vannak, mint az átlag körüliek.
És vannak természetesen extrém alacsonyak és magasak is - de hát pont azért tartjuk "extrémnek" ezeket a nagyon eltérő magasságokat, mert elég ritkák.
A normális eloszlásnak épp ez a lényege: az átlaghoz közeli, átlag körüli értékek a leggyakoribbak, és ahogy távolodunk az átlagtól, egyre kevesebb eset van - mondhatjuk úgy is, minél jobban eltér valami az átlagtól, annál ritkább.
(Folyt. köv.)



A bejegyzés trackback címe:
Kommentek:
A hozzászólások a vonatkozó jogszabályok értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a Felhasználási feltételekben és az adatvédelmi tájékoztatóban.