A program használatának elsajátítása után megtanulhatja a bevitt adatok statisztikai jellemzőinek megjelenítését és azok értelmezését. Az egyes adattípusok mutatóinak táblázása; átlagok csoportonként és változónként, nem átlagolható változók jellemzői. A legalapvetőbb statisztikai és adatkezelési fogalmak szemléletes megértése, és példák bemutatása az SPSS-sel, a kapcsolódó SPSS terminológiák áttekintése.

• a program felépítése, adat-, párbeszéd-, output- és parancs-ablakok
• beállítások, az adatok megjelnítése, és kezelése
• adatbevitel, változók felvétele
• adatok módosítása, ellenőrzése, hiányzó értékek
• leíró statisztikai jellemzők
• a kimenet (output) ablak lehetőségei, navigálás, szerkesztés
• az eredmények megjelenítése, értelmezése, exportálása
• diagramok, grafikonok készítése és szerkesztése

http://spsstanfolyam.hu/?o=spss_tanfolyamok

 Köszönjük a támogatást, a kereséseket: az spsstanfolyam.hu stabilan az első a Google találatai között az "SPSS tanfolyam" kifejezésre.

http://spsstanfolyam.hu/

Egy kis kedvezménnyel szeretnénk kedveskedni ennek örömére: mindenki, aki Google-keresésen át jut el oldalunkra, 10% kedvezményt kap bármely tanfolyamunk vagy szolgáltatásunk árából!

:)

  Ha egy statisztikai tankönyvben megnézzük a normális eloszlás definícióját, valami ilyesmit fogunk látni:

Egy folytonos valószínűségi változót normális eloszlásúnak nevezünk m és s paraméterekkel és N(m ,s )-val jelöljük, ha a sűrűségfüggvénye az ábrának megfelelő.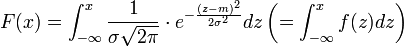

Mond ez valamit egy hétköznapi halandó számára? Nem nagyon. 

Ha valami számszerű jellemzőt akarunk mondani a normális eloszlásra, akkor a legjobb, ha azt vizsgáljuk meg, hogy a korábban említett "átlaghoz közeli", illetve attól távoli értékek milyen arányban fordulnak elő. Vagyis pl. az emberek hányadrésze tartozik az "átlaghoz közeli" csoportba, és hányadrészükre mondható, hogy "extrém" alacsonyak/magasak?

Ehhez egy fogalmat meg kell ismernünk és értenünk: ez a "szórás". A szórás nem más, mint az értékek átlagtól való távolságának (eltérésének) "átlaga" (azért az idézőjel, mert valójában bonyolultabb ennél a számítása, de lényegében ezt fejezi ki).
Ha pl. egy gyerek egy évben kap 3 hármast, 3 négyest, és 3 ötöst, akkor az osztályzatainak az átlaga 4 egész lesz, a szórása 0,82.
(Ha viszont egész évben csak négyesei vannak, akkor - ugyanúgy 4-es átlag mellett - a szórás 0 lesz!)

Nos, normális eloszlásnál az esetek - osztályzatok, testmagasságok stb. - kb. 68%-a az átlagtól számított "egy szóráson" belül lesz, kb. 95%-a "két szóráson" belül, és 99,8%-a "három szóráson" belül.
Ha tehát pl. a magyarországi emberek testmagassága normális eloszlású (elvileg az kell hogy legyen), és az átlagmagasság 170 cm lenne (nem annyi, csak a példa kedvéért), a szórása pedig kerek 20 cm (szintén a példa kedvéért kitalált érték), akkor a kb. 10 millió magyarból 6 millió 800 ezer elvileg 150 és 190 cm között van, 9 és fél millió van 130 és 210 cm között, és nagyjából 9 millió 980 ezer ember még a 110-230 cm határokon belül lenne.

Kedveld a Facebook-lapját a tanfolyamunknak, és Te vagy ismerősöd 10% kedvezményt kap a tanfolyam árából - bármikor is iratkozzon be!   :)

facebook.com/pages/SPSStanfolyam

Hölgyeim és Uraim, ősszel minden(!)  tanfolyamunk elindul, azaz minden szinten (rockandroll...), és minden témában.